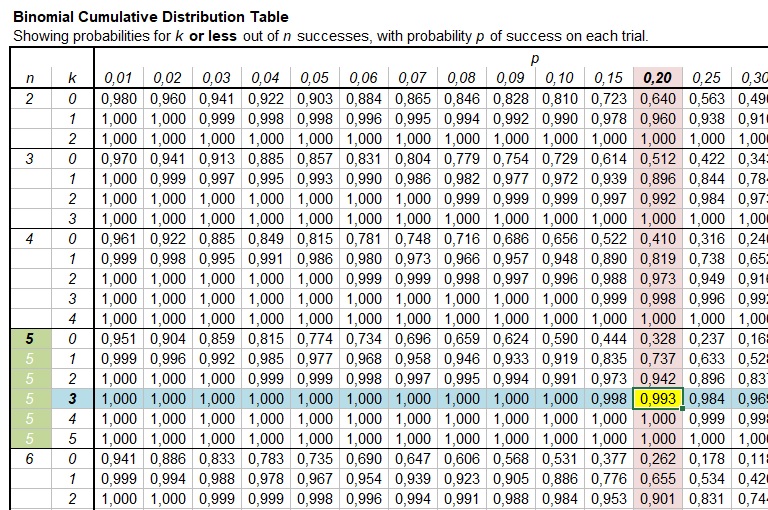
Binomial Distribution Table
Have you ever wondered how probabilities work in situations where there are just two possible outcomes? Think of tossing a coin. Will it be heads or tails? This is where the binomial distribution table comes into play. It’s a handy tool in statistics that helps you calculate the likelihood of specific outcomes. But what exactly is this table, and how can it be used in everyday scenarios? Let’s break it down in a way that’s easy to grasp.
What is a Binomial Distribution?
Before diving into the table itself, it’s important to understand what a binomial distribution is. At its core, a binomial distribution represents the probability of achieving a specific number of “successes” in a fixed number of independent experiments. The key feature of these experiments is that each one has only two possible outcomes—success or failure.
For example, imagine flipping a coin ten times. Each flip can result in either heads or tails. If you wanted to know the probability of getting exactly six heads, the binomial distribution would help you calculate that.
Why Use a Binomial Distribution Table?
Now that you have a sense of what binomial distribution means, you might wonder why a table is necessary. Couldn’t we just do the math each time? Well, technically yes, but it’s not always convenient to perform complex calculations every time you want to know the probability of an event. That’s where the binomial distribution table comes in handy.
A binomial distribution table simplifies the process by giving you pre-calculated probabilities for different scenarios. You just need to know a few key pieces of information, and you can quickly look up the probability rather than calculate it from scratch.
Breaking Down the Table
The binomial distribution table may look overwhelming at first glance, but once you understand how it works, it’s a lifesaver. The table is structured around three main variables:
- n – The number of trials or experiments
- p – The probability of success on a single trial
- x – The number of successes you’re interested in
Each table is typically organized with columns for various values of p (the probability of success) and rows for x (the number of successes). Inside the table, you’ll find the corresponding probabilities for different combinations of n, p, and x.
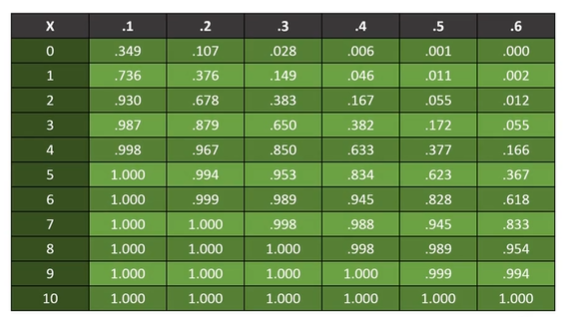
How to Read the Table
Reading a binomial distribution table is like following a simple recipe. Let’s break it down step by step:
- Identify your variables: You need to know how many trials you’re performing (n), the probability of success for each trial (p), and how many successes you’re looking for (x).
- Locate the row for n: Once you know the number of trials, find the corresponding row in the table.
- Find the right column: Move across the row until you find the column that matches the probability of success, p.
- Get your result: The number where the row and column intersect gives you the probability of achieving exactly x successes.
For example, if you’re flipping a coin 5 times (n = 5), and you want to know the probability of getting exactly 3 heads (x = 3) when the probability of success (heads) is 0.5 (p = 0.5), you can simply look up the value in the table.
Real-Life Applications of the Binomial Distribution Table
You might think this table is just a classroom tool, but it’s used in real-world situations more than you’d imagine. Businesses, researchers, and even athletes use it to predict outcomes and make decisions. Let’s explore some practical examples.
Business Decision-Making
In marketing, companies often run campaigns with a set number of customers. They know from past data what percentage of customers typically respond positively. Using the binomial distribution table, they can predict how many customers are likely to respond to the next campaign.
Medical Studies
Researchers in the medical field frequently use binomial distributions to understand the effectiveness of treatments. For instance, in a study with 100 patients, where a treatment has a 70% success rate, the binomial distribution table can help predict the number of patients who will benefit from the treatment.
Sports and Games
Even athletes use binomial distributions without realizing it! Think of basketball players taking a series of free throws. Coaches can predict the likelihood of a player making a certain number of shots, based on past performance, by using the binomial distribution table.
The Math Behind the Table
While the table provides easy-to-access probabilities, it’s good to understand the math behind it, even if you don’t need to calculate it yourself. The binomial probability formula is:P(x)=(nx)⋅px⋅(1−p)n−xP(x) = \binom{n}{x} \cdot p^x \cdot (1 – p)^{n – x}P(x)=(xn)⋅px⋅(1−p)n−x
Where:
- (nx)\binom{n}{x}(xn) is the binomial coefficient, which calculates how many ways you can achieve x successes in n trials.
- pxp^xpx represents the probability of success raised to the power of the number of successes.
- (1−p)n−x(1 – p)^{n – x}(1−p)n−x accounts for the failures in the remaining trials.
This formula might look complex, but the table spares you from doing all these steps manually.
Common Pitfalls to Avoid
While using a binomial distribution table is straightforward, there are a few common mistakes that people often make.
Not Knowing the Exact Values for p and n
The table is built around specific probabilities of success (p) and a fixed number of trials (n). If you don’t have the exact values, the table won’t give you an accurate result. Make sure you’re clear on these numbers before diving into the table.
Confusing Success and Failure
Sometimes it’s easy to confuse what counts as a success versus a failure. For example, in medical studies, is success defined as the treatment working or the treatment failing? Always be clear on how success is defined in your scenario.
Going Beyond the Table
While the binomial distribution table is a great tool, it does have its limitations. For instance, tables are typically only available for certain ranges of n and p. If your situation involves very large numbers, you might need to rely on statistical software or calculators instead of a table.
Additionally, in cases where the probability of success is very low or very high, the binomial distribution may start to resemble other distributions like the Poisson or normal distribution. In these cases, you might need a more advanced approach.
Conclusion: Embracing the Binomial Distribution Table
Whether you’re flipping coins, running a business, or conducting scientific research, the binomial distribution table can simplify your calculations and provide quick insights into the probability of various outcomes. It’s not just a math tool—it’s a practical resource for real-world decision-making. By understanding how to read and use the table, you’ll be better equipped to handle any situation that involves probability, making you a more informed and effective decision-maker.
So the next time you find yourself wondering about the likelihood of a particular event, reach for a binomial distribution table. It might just have the answers you need.







